Consider the language \(\left\{0,1\right\}^*\cdot 0\cdot\left\{0,1\right\}^{n-1}\).
Observe that this language matches all words iff its \(n\)-th last character is \(0\).
- Make an nfa recognising it with at most \(n+1\) states

Start at state \(S\).
- Make a dfa recognising it with exactly \(2^n\) states
As the dfa is large, I will illustrate the idea when \(n=3\).
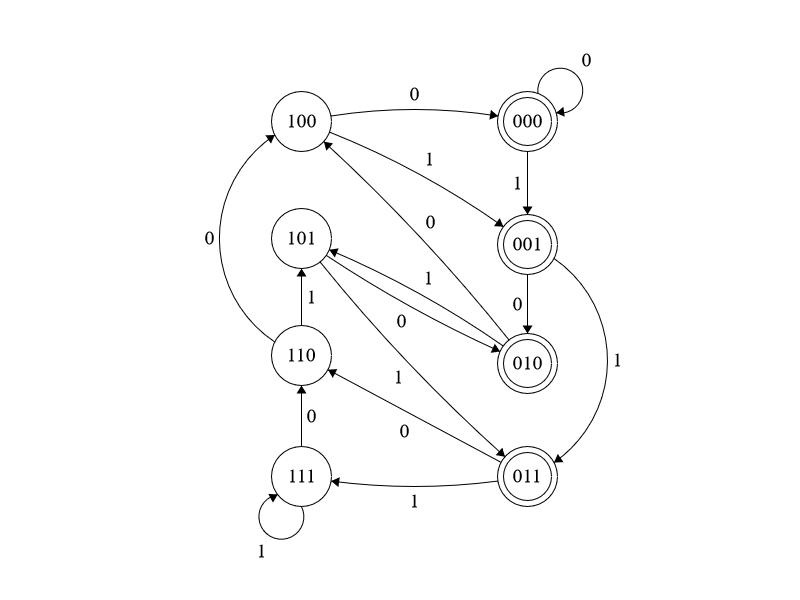
Start at state \(111\).
Note that the transitions follow the rule that the state labelled \(abc\) on character \(d\) transitions to state \(bcd\) for \(a,b,c,d\in\left\{0,1\right\}\).
- Show that a dfa recognising it needs at least \(2^n\) states.
The basic idea is that the dfa must remember the last \(n\)-many characters in order to decide whether a word is in the language or not, this principle is illustrated in my answer for part (c), where the states correspond to \(\left\{0,1\right\}^n\).
To formally prove the lower bound we proceed by showing that \(L = \left\{0,1\right\}^*\cdot 0\cdot\left\{0,1\right\}^{n-1}\) at least has \(2^n\) derivatives, then by theorem of Myhill and Nerode the result follows. Let \(w, w' \in \left\{0,1\right\}^n\), we want to show that \(L_w \ne L_{w'}\). Without loss of generality let \(u,v,u',v'\) such that \[\begin{align*} w &= u0v \\ w' &= u'1v' \\ \left\lvert u\right\rvert &= \left\lvert u'\right\rvert \\ \left\lvert v\right\rvert &= \left\lvert v'\right\rvert \end{align*}\] then we see that \(0^{\left\lvert u\right\rvert} \in L_w\) but \(0^{\left\lvert u\right\rvert} \notin L_{w'}\).